相关分析研究的是现象之间是否相关、相关的方向和密切程度，一般不区别自变量或因变量。而回归分析则要分析现象之间相关的具体形式，确定其因果关系，并用数学模型来表现其具体关系。比如说，从相关分析中我们可以得知“质量”和“用户满意度”变量密切相关，但是这两个变量之间到底是哪个变量受哪个变量的影响，影响程度如何，则需要通过回归分析方法来确定。

一般来说，回归分析是通过规定因变量和自变量来确定变量之间的因果关系，建立回归模型，并根据实测数据来求解模型的各个参数，然后评价回归模型是否能够很好的拟合实测数据；如果能够很好的拟合，则可以根据自变量作进一步预测。

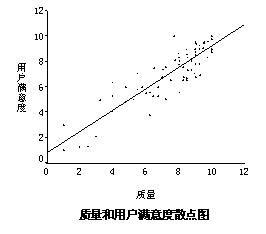
例如，如果要研究质量和用户满意度之间的因果关系，从实践意义上讲，产品质量会影响用户的满意情况，因此设用户满意度为因变量，记为Y；质量为自变量，记为X。根据图8－3的散点图，可以建立下面的线性关系：

    Y=A+BX+§

式中：A和B为待定参数，A为回归直线的截距；B为回归直线的斜率，表示X变化一个单位时，Y的平均变化情况；§为依赖于用户满意度的随机误差项。

在SPSS软件里可以很容易地实现线性回归，回归方程如下：

    y=0.857+0.836x

回归直线在y轴上的截距为0.857、斜率0.836，即质量每提高一分，用户满意度平均上升0.836分；或者说质量每提高1分对用户满意度的贡献是0.836分。

上面所示的例子是简单的一个自变量的线性回归问题，在数据分析的时候，也可以将此推广到多个自变量的多元回归，具体的回归过程和意义请参考相关的统计学书籍。此外，在SPSS的结果输出里，还可以汇报R2，F检验值和T检验值。R2又称为方程的确定性系数（coefficient of determination），表示方程中变量X对Y的解释程度。R2取值在0到1之间，越接近1，表明方程中X对Y的解释能力越强。通常将R2乘以100％来表示回归方程解释Y变化的百分比。F检验是通过方差分析表输出的，通过显著性水平（significant level）检验回归方程的线性关系是否显著。一般来说，显著性水平在0.05以下，均有意义。当F检验通过时，意味着方程中至少有一个回归系数是显著的，但是并不一定所有的回归系数都是显著的，这样就需要通过T检验来验证回归系数的显著性。同样地，T检验可以通过显著性水平或查表来确定。在上面所示的例子中，各参数的意义如表8－2所示。

表8－2  线性回归方程检验

指标		显著性水平	意义
R2	0.89		“质量”解释了89％的“用户满意度”的变化程度
F	276.82	0.001	回归方程的线性关系显著
T	16.64	0.001	回归方程的系数显著

示例  SIM手机用户满意度与相关变量线性回归分析

我们以SIM手机的用户满意度与相关变量的线性回归分析为例，来进一步说明线性回归的应用。从实践意义讲上，手机的用户满意度应该与产品的质量、价格和形象有关，因此我们以“用户满意度”为因变量，“质量”、“形象”和“价格”为自变量，作线性回归分析。利用SPSS软件的回归分析，得到回归方程如下：

用户满意度＝0.008×形象＋0.645×质量＋0.221×价格

对于SIM手机来说，质量对其用户满意度的贡献比较大，质量每提高1分，用户满意度将提高0.645分；其次是价格，用户对价格的评价每提高1分，其满意度将提高0.221分；而形象对产品用户满意度的贡献相对较小，形象每提高1分，用户满意度仅提高0.008分。

方程各检验指标及含义如下：

从方程的检验指标来看，“形象”对整个回归方程的贡献不大，应予以删除。所以重新做“用户满意度”与“质量”、“价格”的回归方程如下：

用户满意度＝0.645×质量＋0.221×价格

对于SIM手机来说，质量对其用户满意度的贡献比较大，质量每提高1分，用户满意度将提高0.645分；用户对价格的评价每提高1分，其满意度将提高0.221分（在本示例中，因为“形象”对方程几乎没有贡献，所以得到的方程与前面的回归方程系数差不多）。

方程各检验指标及含义如下：